اعداد فیبوناچی
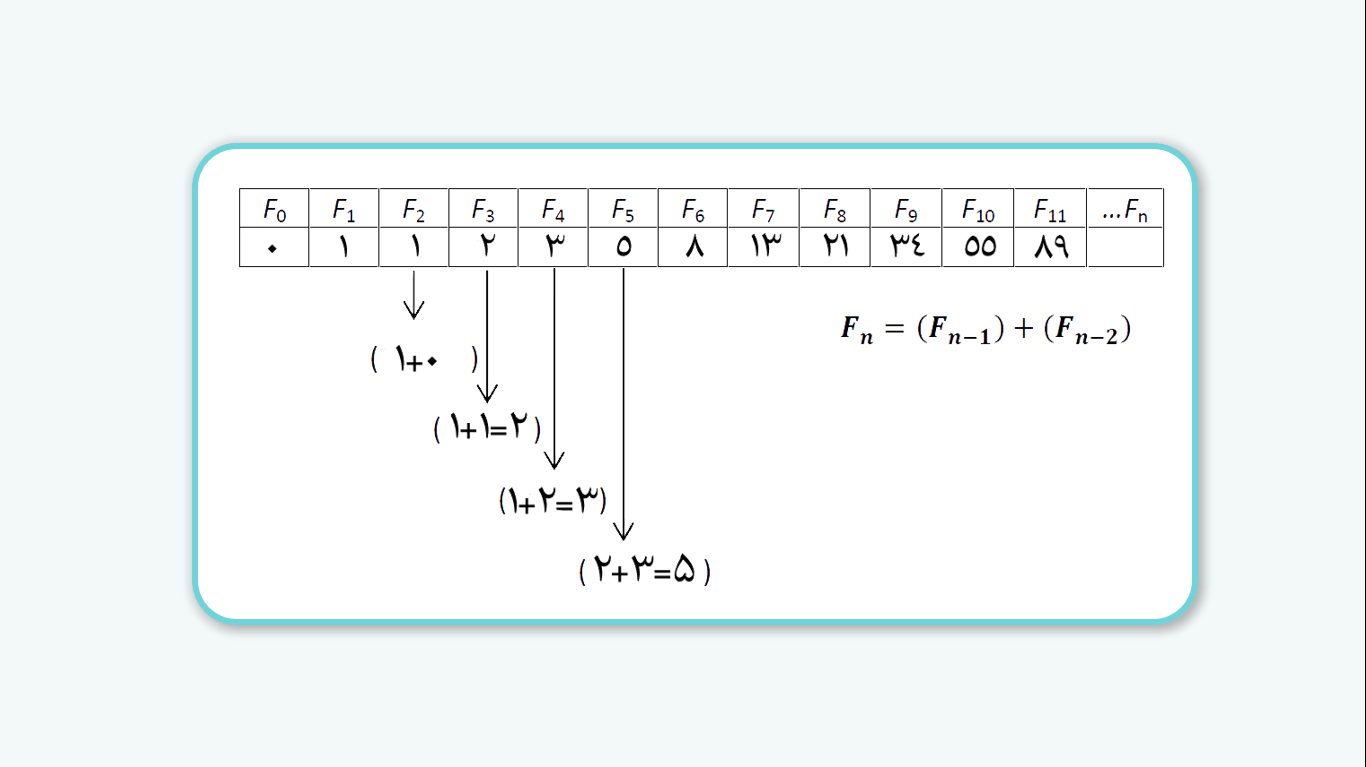
اعداد فیبوناچی مجموعهای از اعداد است که به طور طبیعی در بسیاری از پدیدهها و ساختارهای مختلف ظاهر میشود. این دنباله به گونهای است که هر عدد از مجموع دو عدد قبلی خود به دست میآید. جالب است که این دنباله نه تنها در ریاضیات، بلکه در طبیعت و علوم مختلف نیز کاربردهای گستردهای دارد.
با وجود سادگی در ظاهر، این دنباله ویژگیهای شگفتانگیزی دارد که میتواند به درک بسیاری از الگوها و روابط پیچیدهتر کمک کند. از رشد گیاهان گرفته تا ساختارهای هنری، اعداد فیبوناچی در جایی حضور دارند که به نظر میرسد تنها ارتباط منطقی و ساختاری برای ایجاد نظم و هماهنگی باشد.
تعریف دنباله فیبوناچی
دنباله فیبوناچی به مجموعهای از اعداد گفته میشود که به شکلی خاص با یکدیگر ارتباط دارند. هر عدد در این دنباله به وسیله جمع دو عدد قبلی خود محاسبه میشود. این الگو در ابتدا ممکن است ساده به نظر برسد، اما در واقع ویژگیهای ریاضی و کاربردهای زیادی دارد که آن را در بسیاری از زمینهها برجسته میکند.
ساختار دنباله فیبوناچی
در دنباله فیبوناچی، اولین دو عدد به طور معمول صفر و یک هستند. از اینجا به بعد، هر عدد جدید به دست میآید از طریق جمع دو عدد قبلی خود. به عنوان مثال، دنباله به این شکل ادامه مییابد: ۰، ۱، ۱، ۲، ۳، ۵، ۸، ۱۳ و غیره.
ویژگیهای دنباله فیبوناچی
یکی از ویژگیهای جذاب دنباله فیبوناچی این است که نسبت هر عدد به عدد قبلی خود تقریباً به یک عدد ثابت میرسد که به آن نسبت طلایی گفته میشود. این نسبت در بسیاری از ساختارهای طبیعی و هنری مشاهده میشود.
کاربردهای دنباله فیبوناچی در ریاضیات
دنباله فیبوناچی در ریاضیات کاربردهای فراوانی دارد که از آن به عنوان ابزاری برای حل مسائل مختلف استفاده میشود. این دنباله به عنوان یکی از ساختارهای بنیادین در نظریه اعداد و ترکیبیات شناخته میشود. به ویژه، ویژگیهای خاص این دنباله آن را به ابزاری ارزشمند برای تجزیه و تحلیل مسائل ریاضی پیچیده تبدیل کرده است.
در بسیاری از مسائل، دنباله فیبوناچی میتواند برای مدلسازی پدیدههای رشد، توزیعها و روابط ترکیبیاتی مورد استفاده قرار گیرد. به عنوان مثال، در حل برخی از معادلات دیفرانسیل و مسائل شمارشی، این دنباله به راحتی میتواند به عنوان یک راهحل موثر ظاهر شود.
همچنین، در تحلیل سریهای بینهایت، دنباله فیبوناچی نقش اساسی ایفا میکند. در این زمینه، نسبت طلایی که از این دنباله به دست میآید، در بررسی و حل مسائل ریاضی و هندسی کاربرد دارد. به علاوه، این دنباله در نظریه گرافها و الگوریتمهای جستجو نیز جایگاه ویژهای دارد.
فیبوناچی در طبیعت و زیستشناسی
اعداد فیبوناچی در طبیعت به طور وسیعی مشاهده میشوند و نقش مهمی در شکلگیری بسیاری از الگوهای طبیعی ایفا میکنند. این دنباله به طور غیرقابل انکاری در فرآیندهای زیستی مختلف مانند رشد گیاهان، ترتیب برگها و ساختار موجودات زنده مشاهده میشود. این ارتباط با طبیعت نشاندهنده نوعی نظم در فرآیندهای پیچیده طبیعی است.
ترتیب برگها و گلها

یکی از معروفترین مثالها از کاربرد دنباله فیبوناچی در طبیعت، چیدمان برگها بر روی ساقه گیاهان است. در بسیاری از گیاهان، تعداد برگها یا گلبرگها به گونهای است که در دنباله فیبوناچی قرار میگیرند. این الگو کمک میکند تا گیاهان بیشترین میزان نور خورشید را دریافت کنند و در رشد خود بهینهتر عمل کنند.
ساختار بدن موجودات زنده
دنباله فیبوناچی همچنین در ساختار بدن بسیاری از موجودات زنده مشاهده میشود. به عنوان مثال، تعداد دندانههای حلزونها و صدفها یا الگوی رشد بسیاری از حیوانات به شکلی است که با دنباله فیبوناچی تطابق دارد. این امر نشان میدهد که اصول ریاضی نه تنها در سطح ساختارهای ظاهری، بلکه در فرآیندهای زیستی داخلی نیز موثر است.